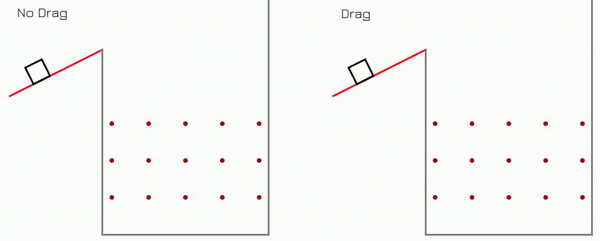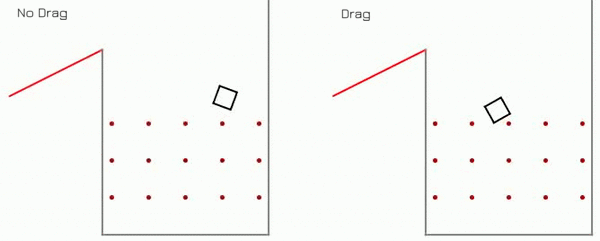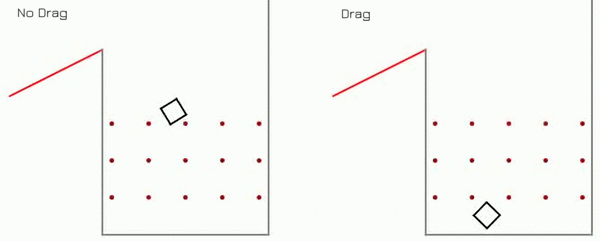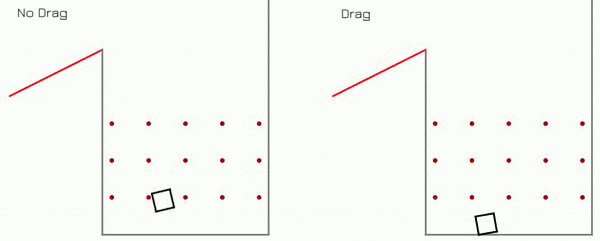
Plinko Game Dynamics
Northwestern University: Machine Dynamics
Technical Skills Used
- Mathematica
- Euler-Lagrange Equations
- Rotational Inertia
- Impact Constraints
- Constrained Dynamics
- External Forces
How it Works
The square prism has the configuration $q=(x,y,\theta)$ and the following dimensions:
- $Height=2h\ along\ the\ z\ axis$
- $Width=2w\ along\ the\ y\ axis$
- $Length=2l\ along\ the\ x\ axis$
The equations that define the Lagrangian Dynamics of the square are described below.
- $KE=\frac{1}{2}{V_{B}}^{T}IV_{B }$
- $PE=mgy$
- $L=KE-PE$
- $V_{B}=\begin{bmatrix}\dot{x} & \dot{y} & \dot{\theta}\end{bmatrix}^{T}$
- $I=\begin{bmatrix}m & 0 & 0\\ 0 & m & 0\\ 0 & 0 & \frac{8}{3}hwl\left ( l^2+w^2 \right )\end{bmatrix}$
The Euler-Lagrange Equations are:
- $\frac{\mathrm{d} }{\mathrm{d} t}\left (\frac{\partial L}{\partial \dot{x}}\right )-\frac{\partial L}{\partial x}=\lambda \frac{\partial \phi}{\partial x}+F_{x}$
- $\frac{\mathrm{d} }{\mathrm{d} t}\left (\frac{\partial L}{\partial \dot{y}}\right )-\frac{\partial L}{\partial y}=\lambda \frac{\partial \phi}{\partial y}+F_{y}$
- $\frac{\mathrm{d} }{\mathrm{d} t}\left (\frac{\partial L}{\partial \dot{\theta}}\right )-\frac{\partial L}{\partial \theta}=\lambda \frac{\partial \phi}{\partial \theta}$
- $F_{x}=\begin{cases}F\cos \theta & \text{ if } x\leq 7 \\ -\frac{1}{2}\rho C_{D} A \dot{x} & \text{ if } x> 7 \end{cases}$
- $F_{y}=\begin{cases}F\sin \theta & \text{ if } x\leq 7 \\ -\frac{1}{2}\rho C_{D} A \dot{y} & \text{ if } x> 7 \end{cases}$
The Impact Constraint Equations are described below.
- $\phi_{x}=x\ coordinate\ \text{of}\ T_{bs}r_{s,pin}=x_{pin}\cos\theta+y_{pin}\sin\theta-x\cos\theta-y\sin\theta$
- $\phi_{y}=y\ coordinate\ \text{of}\ T_{bs}r_{s,pin}=y_{pin}\cos\theta-x_{pin}\sin\theta+x\sin\theta-y\cos\theta$
- $\phi_{x,corner}=x\ coordinate\ \text{of}\ T_{sb}r_{b,pin}=\begin{cases}l\cos\theta-w\sin\theta+x & \text{ if } (x_{b},y_{b})= (l,w)\\ l\cos\theta+w\sin\theta+x & \text{ if } (x_{b},y_{b})= (l,-w)\\-l\cos\theta+w\sin\theta+x & \text{ if } (x_{b},y_{b})= (-l,-w)\\-l\cos\theta-w\sin\theta+x & \text{ if } (x_{b},y_{b})= (-l,w)\\\end{cases}$
- $\phi_{y,corner}=y\ coordinate\ \text{of}\ T_{sb}r_{b,pin}=\begin{cases}w\cos\theta+l\sin\theta+y & \text{ if } (x_{b},y_{b})= (l,w)\\ -w\cos\theta+l\sin\theta+y & \text{ if } (x_{b},y_{b})= (l,-w)\\-w\cos\theta-l\sin\theta+y & \text{ if } (x_{b},y_{b})= (-l,-w)\\w\cos\theta-l\sin\theta+y & \text{ if } (x_{b},y_{b})= (-l,w)\\\end{cases}$
The Impact Update Laws are described below.
- $\frac{\partial L}{\partial \dot{x}}_{\tau^{+}}-\frac{\partial L}{\partial \dot{x}}_{\tau^{-}}=\lambda \frac{\partial \phi}{\partial x}$
- $\frac{\partial L}{\partial \dot{y}}_{\tau^{+}}-\frac{\partial L}{\partial \dot{y}}_{\tau^{-}}=\lambda \frac{\partial \phi}{\partial y}$
- $\frac{\partial L}{\partial \dot{\theta}}_{\tau^{+}}-\frac{\partial L}{\partial \dot{\theta}}_{\tau^{-}}=\lambda \frac{\partial \phi}{\partial \theta}$
- $H_{\tau^{+}}-H_{\tau^{-}}=0$
The Impact Update Laws are called when the following events occur:
- $\text{If} \left | \phi_{x} \right | -l-radius_{pin}=0\ \text{and}\ \left | \phi_{y} \right | -w-radius_{pin}=0 \\ \text{then update}\ {x}',{y}',{\theta}'\ \text{using the update laws with}\ \phi=\phi_{x}\ \text{and}\ \phi=\phi_{y}$
- $\text{If}\ \phi_{x,corner} -7=0\ \text{or}\ \phi_{x,corner} -25=0\\ \text{then update}\ {x}',{y}',{\theta}'\ \text{using the update laws with}\ \phi= \phi_{x,corner}$
- $\text{If}\ \phi_{y,corner} =0\\ \text{then update}\ {x}',{y}',{\theta}'\ \text{using the update laws with}\ \phi= \phi_{y,corner}$
Demo